Artnemiz1
Shared posts
Saturday Morning Breakfast Cereal - Hubris

Click here to go see the bonus panel!
Hovertext:
If you're more irritated about the geographical location of the penguins than the fact that the penguins can talk, I have nothing to say to you.
New comic!
Today's News:
Saturday Morning Breakfast Cereal - Quantum Weirdness

Click here to go see the bonus panel!
Hovertext:
Weinersmith spent Christmas accusing God of things, as was his wont.
New comic!
Today's News:
Quantum Theory Rebuilt From Simple Physical Principles
Scientists have been using quantum theory for almost a century now, but embarrassingly they still don’t know what it means. An informal poll taken at a 2011 conference on Quantum Physics and the Nature of Reality showed that there’s still no consensus on what quantum theory says about reality — the participants remained deeply divided about how the theory should be interpreted.
Some physicists just shrug and say we have to live with the fact that quantum mechanics is weird. So particles can be in two places at once, or communicate instantaneously over vast distances? Get over it. After all, the theory works fine. If you want to calculate what experiments will reveal about subatomic particles, atoms, molecules and light, then quantum mechanics succeeds brilliantly.
But some researchers want to dig deeper. They want to know why quantum mechanics has the form it does, and they are engaged in an ambitious program to find out. It is called quantum reconstruction, and it amounts to trying to rebuild the theory from scratch based on a few simple principles.
If these efforts succeed, it’s possible that all the apparent oddness and confusion of quantum mechanics will melt away, and we will finally grasp what the theory has been trying to tell us. “For me, the ultimate goal is to prove that quantum theory is the only theory where our imperfect experiences allow us to build an ideal picture of the world,” said Giulio Chiribella, a theoretical physicist at the University of Hong Kong.
There’s no guarantee of success — no assurance that quantum mechanics really does have something plain and simple at its heart, rather than the abstruse collection of mathematical concepts used today. But even if quantum reconstruction efforts don’t pan out, they might point the way to an equally tantalizing goal: getting beyond quantum mechanics itself to a still deeper theory. “I think it might help us move towards a theory of quantum gravity,” said Lucien Hardy, a theoretical physicist at the Perimeter Institute for Theoretical Physics in Waterloo, Canada.

The Flimsy Foundations of Quantum Mechanics
The basic premise of the quantum reconstruction game is summed up by the joke about the driver who, lost in rural Ireland, asks a passer-by how to get to Dublin. “I wouldn’t start from here,” comes the reply.
Where, in quantum mechanics, is “here”? The theory arose out of attempts to understand how atoms and molecules interact with light and other radiation, phenomena that classical physics couldn’t explain. Quantum theory was empirically motivated, and its rules were simply ones that seemed to fit what was observed. It uses mathematical formulas that, while tried and trusted, were essentially pulled out of a hat by the pioneers of the theory in the early 20th century.
Take Erwin Schrödinger’s equation for calculating the probabilistic properties of quantum particles. The particle is described by a “wave function” that encodes all we can know about it. It’s basically a wavelike mathematical expression, reflecting the well-known fact that quantum particles can sometimes seem to behave like waves. Want to know the probability that the particle will be observed in a particular place? Just calculate the square of the wave function (or, to be exact, a slightly more complicated mathematical term), and from that you can deduce how likely you are to detect the particle there. The probability of measuring some of its other observable properties can be found by, crudely speaking, applying a mathematical function called an operator to the wave function.
But this so-called rule for calculating probabilities was really just an intuitive guess by the German physicist Max Born. So was Schrödinger’s equation itself. Neither was supported by rigorous derivation. Quantum mechanics seems largely built of arbitrary rules like this, some of them — such as the mathematical properties of operators that correspond to observable properties of the system — rather arcane. It’s a complex framework, but it’s also an ad hoc patchwork, lacking any obvious physical interpretation or justification.
Compare this with the ground rules, or axioms, of Einstein’s theory of special relativity, which was as revolutionary in its way as quantum mechanics. (Einstein launched them both, rather miraculously, in 1905.) Before Einstein, there was an untidy collection of equations to describe how light behaves from the point of view of a moving observer. Einstein dispelled the mathematical fog with two simple and intuitive principles: that the speed of light is constant, and that the laws of physics are the same for two observers moving at constant speed relative to one another. Grant these basic principles, and the rest of the theory follows. Not only are the axioms simple, but we can see at once what they mean in physical terms.
What are the analogous statements for quantum mechanics? The eminent physicist John Wheeler once asserted that if we really understood the central point of quantum theory, we would be able to state it in one simple sentence that anyone could understand. If such a statement exists, some quantum reconstructionists suspect that we’ll find it only by rebuilding quantum theory from scratch: by tearing up the work of Bohr, Heisenberg and Schrödinger and starting again.

Quantum Roulette
One of the first efforts at quantum reconstruction was made in 2001 by Hardy, then at the University of Oxford. He ignored everything that we typically associate with quantum mechanics, such as quantum jumps, wave-particle duality and uncertainty. Instead, Hardy focused on probability: specifically, the probabilities that relate the possible states of a system with the chance of observing each state in a measurement. Hardy found that these bare bones were enough to get all that familiar quantum stuff back again.
Hardy assumed that any system can be described by some list of properties and their possible values. For example, in the case of a tossed coin, the salient values might be whether it comes up heads or tails. Then he considered the possibilities for measuring those values definitively in a single observation. You might think any distinct state of any system can always be reliably distinguished (at least in principle) by a measurement or observation. And that’s true for objects in classical physics.
In quantum mechanics, however, a particle can exist not just in distinct states, like the heads and tails of a coin, but in a so-called superposition — roughly speaking, a combination of those states. In other words, a quantum bit, or qubit, can be not just in the binary state of 0 or 1, but in a superposition of the two.
But if you make a measurement of that qubit, you’ll only ever get a result of 1 or 0. That is the mystery of quantum mechanics, often referred to as the collapse of the wave function: Measurements elicit only one of the possible outcomes. To put it another way, a quantum object commonly has more options for measurements encoded in the wave function than can be seen in practice.
Hardy’s rules governing possible states and their relationship to measurement outcomes acknowledged this property of quantum bits. In essence the rules were (probabilistic) ones about how systems can carry information and how they can be combined and interconverted.
Hardy then showed that the simplest possible theory to describe such systems is quantum mechanics, with all its characteristic phenomena such as wavelike interference and entanglement, in which the properties of different objects become interdependent. “Hardy’s 2001 paper was the ‘Yes, we can!’ moment of the reconstruction program,” Chiribella said. “It told us that in some way or another we can get to a reconstruction of quantum theory.”
More specifically, it implied that the core trait of quantum theory is that it is inherently probabilistic. “Quantum theory can be seen as a generalized probability theory, an abstract thing that can be studied detached from its application to physics,” Chiribella said. This approach doesn’t address any underlying physics at all, but just considers how outputs are related to inputs: what we can measure given how a state is prepared (a so-called operational perspective). “What the physical system is is not specified and plays no role in the results,” Chiribella said. These generalized probability theories are “pure syntax,” he added — they relate states and measurements, just as linguistic syntax relates categories of words, without regard to what the words mean. In other words, Chiribella explained, generalized probability theories “are the syntax of physical theories, once we strip them of the semantics.”
The general idea for all approaches in quantum reconstruction, then, is to start by listing the probabilities that a user of the theory assigns to each of the possible outcomes of all the measurements the user can perform on a system. That list is the “state of the system.” The only other ingredients are the ways in which states can be transformed into one another, and the probability of the outputs given certain inputs. This operational approach to reconstruction “doesn’t assume space-time or causality or anything, only a distinction between these two types of data,” said Alexei Grinbaum, a philosopher of physics at the CEA Saclay in France.
To distinguish quantum theory from a generalized probability theory, you need specific kinds of constraints on the probabilities and possible outcomes of measurement. But those constraints aren’t unique. So lots of possible theories of probability look quantum-like. How then do you pick out the right one?
“We can look for probabilistic theories that are similar to quantum theory but differ in specific aspects,” said Matthias Kleinmann, a theoretical physicist at the University of the Basque Country in Bilbao, Spain. If you can then find postulates that select quantum mechanics specifically, he explained, you can “drop or weaken some of them and work out mathematically what other theories appear as solutions.” Such exploration of what lies beyond quantum mechanics is not just academic doodling, for it’s possible — indeed, likely — that quantum mechanics is itself just an approximation of a deeper theory. That theory might emerge, as quantum theory did from classical physics, from violations in quantum theory that appear if we push it hard enough.

Bits and Pieces
Some researchers suspect that ultimately the axioms of a quantum reconstruction will be about information: what can and can’t be done with it. One such derivation of quantum theory based on axioms about information was proposed in 2010 by Chiribella, then working at the Perimeter Institute, and his collaborators Giacomo Mauro D’Ariano and Paolo Perinotti of the University of Pavia in Italy. “Loosely speaking,” explained Jacques Pienaar, a theoretical physicist at the University of Vienna, “their principles state that information should be localized in space and time, that systems should be able to encode information about each other, and that every process should in principle be reversible, so that information is conserved.” (In irreversible processes, by contrast, information is typically lost — just as it is when you erase a file on your hard drive.)
What’s more, said Pienaar, these axioms can all be explained using ordinary language. “They all pertain directly to the elements of human experience, namely, what real experimenters ought to be able to do with the systems in their laboratories,” he said. “And they all seem quite reasonable, so that it is easy to accept their truth.” Chiribella and his colleagues showed that a system governed by these rules shows all the familiar quantum behaviors, such as superposition and entanglement.
One challenge is to decide what should be designated an axiom and what physicists should try to derive from the axioms. Take the quantum no-cloning rule, which is another of the principles that naturally arises from Chiribella’s reconstruction. One of the deep findings of modern quantum theory, this principle states that it is impossible to make a duplicate of an arbitrary, unknown quantum state.
It sounds like a technicality (albeit a highly inconvenient one for scientists and mathematicians seeking to design quantum computers). But in an effort in 2002 to derive quantum mechanics from rules about what is permitted with quantum information, Jeffrey Bub of the University of Maryland and his colleagues Rob Clifton of the University of Pittsburgh and Hans Halvorson of Princeton University made no-cloning one of three fundamental axioms. One of the others was a straightforward consequence of special relativity: You can’t transmit information between two objects more quickly than the speed of light by making a measurement on one of the objects. The third axiom was harder to state, but it also crops up as a constraint on quantum information technology. In essence, it limits how securely a bit of information can be exchanged without being tampered with: The rule is a prohibition on what is called “unconditionally secure bit commitment.”
These axioms seem to relate to the practicalities of managing quantum information. But if we consider them instead to be fundamental, and if we additionally assume that the algebra of quantum theory has a property called non-commutation, meaning that the order in which you do calculations matters (in contrast to the multiplication of two numbers, which can be done in any order), Clifton, Bub and Halvorson have shown that these rules too give rise to superposition, entanglement, uncertainty, nonlocality and so on: the core phenomena of quantum theory.
Another information-focused reconstruction was suggested in 2009 by Borivoje Dakić and Časlav Brukner, physicists at the University of Vienna. They proposed three “reasonable axioms” having to do with information capacity: that the most elementary component of all systems can carry no more than one bit of information, that the state of a composite system made up of subsystems is completely determined by measurements on its subsystems, and that you can convert any “pure” state to another and back again (like flipping a coin between heads and tails).
Dakić and Brukner showed that these assumptions lead inevitably to classical and quantum-style probability, and to no other kinds. What’s more, if you modify axiom three to say that states get converted continuously — little by little, rather than in one big jump — you get only quantum theory, not classical. (Yes, it really is that way round, contrary to what the “quantum jump” idea would have you expect — you can interconvert states of quantum spins by rotating their orientation smoothly, but you can’t gradually convert a classical heads to a tails.) “If we don’t have continuity, then we don’t have quantum theory,” Grinbaum said.
A further approach in the spirit of quantum reconstruction is called quantum Bayesianism, or QBism. Devised by Carlton Caves, Christopher Fuchs and Rüdiger Schack in the early 2000s, it takes the provocative position that the mathematical machinery of quantum mechanics has nothing to do with the way the world really is; rather, it is just the appropriate framework that lets us develop expectations and beliefs about the outcomes of our interventions. It takes its cue from the Bayesian approach to classical probability developed in the 18th century, in which probabilities stem from personal beliefs rather than observed frequencies. In QBism, quantum probabilities calculated by the Born rule don’t tell us what we’ll measure, but only what we should rationally expect to measure.
In this view, the world isn’t bound by rules — or at least, not by quantum rules. Indeed, there may be no fundamental laws governing the way particles interact; instead, laws emerge at the scale of our observations. This possibility was considered by John Wheeler, who dubbed the scenario Law Without Law. It would mean that “quantum theory is merely a tool to make comprehensible a lawless slicing-up of nature,” said Adán Cabello, a physicist at the University of Seville. Can we derive quantum theory from these premises alone?
“At first sight, it seems impossible,” Cabello admitted — the ingredients seem far too thin, not to mention arbitrary and alien to the usual assumptions of science. “But what if we manage to do it?” he asked. “Shouldn’t this shock anyone who thinks of quantum theory as an expression of properties of nature?”

Making Space for Gravity
In Hardy’s view, quantum reconstructions have been almost too successful, in one sense: Various sets of axioms all give rise to the basic structure of quantum mechanics. “We have these different sets of axioms, but when you look at them, you can see the connections between them,” he said. “They all seem reasonably good and are in a formal sense equivalent because they all give you quantum theory.” And that’s not quite what he’d hoped for. “When I started on this, what I wanted to see was two or so obvious, compelling axioms that would give you quantum theory and which no one would argue with.”
So how do we choose between the options available? “My suspicion now is that there is still a deeper level to go to in understanding quantum theory,” Hardy said. And he hopes that this deeper level will point beyond quantum theory, to the elusive goal of a quantum theory of gravity. “That’s the next step,” he said. Several researchers working on reconstructions now hope that its axiomatic approach will help us see how to pose quantum theory in a way that forges a connection with the modern theory of gravitation — Einstein’s general relativity.
Look at the Schrödinger equation and you will find no clues about how to take that step. But quantum reconstructions with an “informational” flavor speak about how information-carrying systems can affect one another, a framework of causation that hints at a link to the space-time picture of general relativity. Causation imposes chronological ordering: An effect can’t precede its cause. But Hardy suspects that the axioms we need to build quantum theory will be ones that embrace a lack of definite causal structure — no unique time-ordering of events — which he says is what we should expect when quantum theory is combined with general relativity. “I’d like to see axioms that are as causally neutral as possible, because they’d be better candidates as axioms that come from quantum gravity,” he said.
Hardy first suggested that quantum-gravitational systems might show indefinite causal structure in 2007. And in fact only quantum mechanics can display that. While working on quantum reconstructions, Chiribella was inspired to propose an experiment to create causal superpositions of quantum systems, in which there is no definite series of cause-and-effect events. This experiment has now been carried out by Philip Walther’s lab at the University of Vienna — and it might incidentally point to a way of making quantum computing more efficient.
“I find this a striking illustration of the usefulness of the reconstruction approach,” Chiribella said. “Capturing quantum theory with axioms is not just an intellectual exercise. We want the axioms to do something useful for us — to help us reason about quantum theory, invent new communication protocols and new algorithms for quantum computers, and to be a guide for the formulation of new physics.”
But can quantum reconstructions also help us understand the “meaning” of quantum mechanics? Hardy doubts that these efforts can resolve arguments about interpretation — whether we need many worlds or just one, for example. After all, precisely because the reconstructionist program is inherently “operational,” meaning that it focuses on the “user experience” — probabilities about what we measure — it may never speak about the “underlying reality” that creates those probabilities.
“When I went into this approach, I hoped it would help to resolve these interpretational problems,” Hardy admitted. “But I would say it hasn’t.” Cabello agrees. “One can argue that previous reconstructions failed to make quantum theory less puzzling or to explain where quantum theory comes from,” he said. “All of them seem to miss the mark for an ultimate understanding of the theory.” But he remains optimistic: “I still think that the right approach will dissolve the problems and we will understand the theory.”
Maybe, Hardy said, these challenges stem from the fact that the more fundamental description of reality is rooted in that still undiscovered theory of quantum gravity. “Perhaps when we finally get our hands on quantum gravity, the interpretation will suggest itself,” he said. “Or it might be worse!”
Right now, quantum reconstruction has few adherents — which pleases Hardy, as it means that it’s still a relatively tranquil field. But if it makes serious inroads into quantum gravity, that will surely change. In the 2011 poll, about a quarter of the respondents felt that quantum reconstructions will lead to a new, deeper theory. A one-in-four chance certainly seems worth a shot.
Grinbaum thinks that the task of building the whole of quantum theory from scratch with a handful of axioms may ultimately be unsuccessful. “I’m now very pessimistic about complete reconstructions,” he said. But, he suggested, why not try to do it piece by piece instead — to just reconstruct particular aspects, such as nonlocality or causality? “Why would one try to reconstruct the entire edifice of quantum theory if we know that it’s made of different bricks?” he asked. “Reconstruct the bricks first. Maybe remove some and look at what kind of new theory may emerge.”
“I think quantum theory as we know it will not stand,” Grinbaum said. “Which of its feet of clay will break first is what reconstructions are trying to explore.” He thinks that, as this daunting task proceeds, some of the most vexing and vague issues in standard quantum theory — such as the process of measurement and the role of the observer — will disappear, and we’ll see that the real challenges are elsewhere. “What is needed is new mathematics that will render these notions scientific,” he said. Then, perhaps, we’ll understand what we’ve been arguing about for so long.

This article was reprinted on Wired.com.
Saturday Morning Breakfast Cereal - Rain

Click here to go see the bonus panel!
Hovertext:
Mammatus clouds are what God watches when He's getting high.
New comic!
Today's News:
I think B&N is only opening up 1,000 of these, so if you want one, now's the time!
Saturday Morning Breakfast Cereal - I Know Nothing

Click here to go see the bonus panel!
Hovertext:
Look, it's like 400 BC. All of math is a couple theorems for plane geometry and maybe some number theory.
New comic!
Today's News:
Just twooooo short weeks left to get your proposal in for BAHFest Seattle or BAHFest San Francisco! We are always looking for more submissions from women, so please nudge your nerdy ladyfriends!
Highlights from Artist Tatsuya Tanaka’s Daily Miniature Photo Project

Photographer and art director Tatsuya Tanaka has a fascination with all things tiny and has an uncanny ability to repurpose everyday objects as set pieces or tools for the inhabitants of his miniature world. For his project Miniature Calendar, Tanaka has been stretching his imagination to its limits nearly every day for the last four years. A tape dispenser becomes the bar for a restaurant, a circuit board is suddenly a rice paddy field, and the notes of a musical score become the hurdles for a track race. Individually, the photos might invoke a smile or chuckle as you get the joke, but when viewed collectively they morph into a fascinating study on Tanaka’s breadth of creativity.
New photos from Miniature Calendar are published every day on Instagram and Facebook. Tanaka also published a book of earlier miniature photos in a book titled Miniature Life. (via Spoon & Tamago)






Saturday Morning Breakfast Cereal - Dead
.png)
Click here to go see the bonus panel!
Hovertext:
I dare anyone out there to spend 30 years becoming a respected figure in a religious community, then ruin it all by doing this. I'll give you 100 Internet points.
New comic!
Today's News:
Only 30% of tickets are left if you wanna see me, Marc Abrahams and more at BAHFest MIT!
209. FRIDA KAHLO: Heroine of pain
Artnemiz1Una corta biografia de los malestares de Frida Kahlo....
Next time you complain that you don’t know what your passion is or are wondering where to apply your creativity, count your blessings you didn’t have go through a horrifying bus accident to find some clarity.
By all accounts, the young Frida Kahlo’s career plan was to become a doctor. She was a bright young woman and attended Mexico’s prestigious National Preparatory School where she was only one of 35 female students among 2000. She was in her senior year and making plans to attend medical school when the fateful day of the bus accident occurred.
Yes, she had dabbled in art before. Frida’s father, whom she greatly admired, was an amateur artist and she began to draw at age 12, but the accident and the isolation of her recovery changed Frida. Trapped in bed for months, she re-evaluated not only herself but the world around her. With the help of a mirror placed above her bed, Frida began painting self-portraits, something she would do for the rest of her life, constantly examining herself and looking inward. After the tragedy of the accident Frida was reborn and had found new life in painting: “From that time my obsession was to begin again, painting things just as I saw them with my own eyes and nothing more.”
It’s an origin story befitting a superhero, and Frida continued to live a heroic life despite decades of more agony and suffering (shortly after her exhibition in Mexico, her right leg had to be amputated below the knee due to gangrene). She really was “la heroina del dolor”, the Heroine of Pain.
RELATED COMICS
Make Good Art
Strange Like Me
The Blank Canvas
The Bell Jar
Frida’s work was small and personal compared to her husband Diego’s massive murals. During her life, she was always just seen by the public as “the wife of Diego”. This patronising news article from 1933 titled Wife of the Master Mural Painter Gleefully Dabbles in Works of Art will give you an idea of what she dealt with. Aw isn’t that cute, the wife paints too! I wonder how Diego would feel today knowing that his wife has far surpassed him in fame and has become a cultural icon.
Saturday Morning Breakfast Cereal - The Uses of Bureaucracy

Click here to go see the bonus panel!
Hovertext:
Look, I don't know what I was thinking when I drew his hair. I guess he stopped off at an expensive salon on the way home.
New comic!
Today's News:
Why Did Life Move to Land? For the View
Artnemiz1El mejor apellido... : "Being something of a polymath, with interests and experience in robotics and mathematics in addition to biology, neuroscience and paleontology, MacIver built a robotic version of the knifefish, complete with an electrosensory system, to study its exotic sensing abilities and its unusually agile movement."
Life on Earth began in the water. So when the first animals moved onto land, they had to trade their fins for limbs, and their gills for lungs, the better to adapt to their new terrestrial environment.
A new study, out today, suggests that the shift to lungs and limbs doesn’t tell the full story of these creatures’ transformation. As they emerged from the sea, they gained something perhaps more precious than oxygenated air: information. In air, eyes can see much farther than they can under water. The increased visual range provided an “informational zip line” that alerted the ancient animals to bountiful food sources near the shore, according to Malcolm MacIver, a neuroscientist and engineer at Northwestern University.
This zip line, MacIver maintains, drove the selection of rudimentary limbs, which allowed animals to make their first brief forays onto land. Furthermore, it may have had significant implications for the emergence of more advanced cognition and complex planning. “It’s hard to look past limbs and think that maybe information, which doesn’t fossilize well, is really what brought us onto land,” MacIver said.
MacIver and Lars Schmitz, a paleontologist at the Claremont Colleges, have created mathematical models that explore how the increase in information available to air-dwelling creatures would have manifested itself, over the eons, in an increase in eye size. They describe the experimental evidence they have amassed to support what they call the “buena vista” hypothesis in the Proceedings of the National Academy of Sciences.
MacIver’s work is already earning praise from experts in the field for its innovative and thorough approach. While paleontologists have long speculated about eye size in fossils and what that can tell us about an animal’s vision, “this takes it a step further,” said John Hutchinson of the Royal Veterinary College in the U.K. “It isn’t just telling stories based on qualitative observations; it’s testing assumptions and tracking big changes quantitatively over macro-evolutionary time.”
Underwater Hunters
MacIver first came up with his hypothesis in 2007 while studying the black ghost knifefish of South America — an electric fish that hunts at night by generating electrical currents in the water to sense its environment. MacIver compares the effect to a kind of radar system. Being something of a polymath, with interests and experience in robotics and mathematics in addition to biology, neuroscience and paleontology, MacIver built a robotic version of the knifefish, complete with an electrosensory system, to study its exotic sensing abilities and its unusually agile movement.
When MacIver compared the volume of space in which the knifefish can potentially detect water fleas, one of its favorite prey, with that of a fish that relies on vision to hunt the same prey, he found they were roughly the same. This was surprising. Because the knifefish must generate electricity to perceive the world — something that requires a lot of energy — he expected it would have a smaller sensory volume for prey compared to that of a vision-centric fish. At first he thought he had made a simple calculation error. But he soon discovered that the critical factor accounting for the unexpectedly small visual sensory space was the amount that water absorbs and scatters light. In fresh shallow water, for example, the “attenuation length” that light can travel before it is scattered or absorbed ranges from 10 centimeters to two meters. In air, light can travel between 25 to 100 kilometers, depending on how much moisture is in the air.
Because of this, aquatic creatures rarely gain much evolutionary benefit from an increase in eye size, and they have much to lose. Eyes are costly in evolutionary terms because they require so much energy to maintain; photoreceptor cells and neurons in the visual areas of the brain need a lot of oxygen to function. Therefore, any increase in eye size had better yield significant benefits to justify that extra energy. MacIver likens increasing eye size in the water to switching on high beams in the fog in an attempt to see farther ahead.
But once you take eyes out of the water and into air, a larger eye size leads to a proportionate increase in how far you can see.
[No Caption]
MacIver concluded that eye size would have increased significantly during the water-to-land transition. When he mentioned his insight to the evolutionary biologist Neil Shubin — a member of the team that discovered Tiktaalik roseae, an important transitional fossil from 375 million years ago that had lungs and gills — MacIver was encouraged to learn that paleontologists had noticed an increase in eye size in the fossil record. They just hadn’t ascribed much significance to the change. MacIver decided to investigate for himself.
Crocodile Eyes
MacIver had an intriguing hypothesis, but he needed evidence. He teamed up with Schmitz, who had expertise in interpreting the eye sockets of four-legged “tetrapod” fossils (of which Tiktaalik was one), and the two scientists pondered how best to test MacIver’s idea.
MacIver and Schmitz first made a careful review of the fossil record to track changes in the size of eye sockets, which would indicate corresponding changes in eyes, since they are proportional to socket size. The pair collected 59 early tetrapod skulls spanning the water-to-land transition period that were sufficiently intact to allow them to measure both the eye orbit and the length of the skull. Then they fed those data into a computer model to simulate how eye socket size changed over many generations, so as to gain a sense of the evolutionary genetic drift of that trait.
They found that there was indeed a marked increase in eye size — a tripling, in fact — during the transitional period. The average eye socket size before transition was 13 millimeters, compared to 36 millimeters after. Furthermore, in those creatures that went from water to land and back to the water — like the Mexican cave fish Astyanax mexicanus — the mean orbit size shrank back to 14 millimeters, nearly the same as it had been before.
There was just one problem with these results. Originally, MacIver had assumed that the increase occurred after animals became fully terrestrial, since the evolutionary benefits of being able to see farther on land would have led to the increase in eye socket size. But the shift occurred before the water-to-land transition was complete, even before creatures developed rudimentary digits on their fishlike appendages. So how could being on land have driven the gradual increase in eye socket size?
When they reviewed their data on eye size in the fossil record, MacIver and Schmitz noticed that the orbits shifted position over the transitional period, from the sides of the skull to the top, where they were mounted on bony prominences. They also observed tiny notches near the ear area called “spiracles,” designed to make it easier for the tetrapods to breathe through air. In short, the creatures resembled crocodiles. Suddenly, everything clicked into place. “I hadn’t anticipated that these creatures may have used aerial vision while still being aquatic,” MacIver said. “I assumed aerial vision equaled being on land. It doesn’t.” Rather, transitional tetrapods would have hunted like crocodiles, lurking in the shore’s shallow waters, with just the eyes peeking above the surface, lunging onto land whenever they spotted tasty prey.
In that case, “it looks like hunting like a crocodile was the gateway drug to terrestriality,” MacIver said. “Just as data comes before action, coming up on land was likely about how the huge gain in visual performance from poking eyes above the water to see an unexploited source of prey gradually selected for limbs.”
This insight is consistent with the work of Jennifer Clack, a paleontologist at the University of Cambridge, on a fossil known as Pederpes finneyae, which had the oldest known foot for walking on land, yet was not a truly terrestrial creature. While early tetrapods were primarily aquatic, and later tetrapods were clearly terrestrial, paleontologists believe this creature likely spent time in water and on land.
After determining how much eye sizes increased, MacIver set out to calculate how much farther the animals could see with bigger eyes. He adapted an existing ecological model that takes into account not just the anatomy of the eye, but other factors such as the surrounding environment. In water, a larger eye only increases the visual range from just over six meters to nearly seven meters. But increase the eye size in air, and the improvement in range goes from 200 meters to 600 meters.
MacIver and Schmitz ran the same simulation under many different conditions: daylight, a moonless night, starlight, clear water and murky water. “It doesn’t matter,” MacIver said. “In all cases, the increment [in air] is huge. Even if they were hunting in broad daylight in the water and only came out on moonless nights, it’s still advantageous for them, vision-wise.”
Using quantitative tools to help explain patterns in the fossil record is something of a novel approach to the problem, but a growing number of paleontologists and evolutionary biologists, like Schmitz, are embracing these methods.
“So much of paleontology is looking at fossils and then making up narratives on how the fossils might have fit into a particular environment,” said John Long, a paleobiologist at Flinders University in Australia who studies how fish evolved into tetrapods. “This paper has very good hard experimental data, testing vision in different environments. And that data does fit the patterns that we see in these fish.”
Schmitz identified two key developments in the quantitative approach over the past decade. First, more scientists have been adapting methods from modern comparative biology to fossil record analysis, studying how animals are related to each other. Second, there is a lot of interest in modeling the biomechanics of ancient creatures in a way that is actually testable — to determine how fast dinosaurs could run, for instance. Such a model-based approach to interpreting fossils can be applied not only to biomechanics but to sensory function — in this case, it explained how coming out of the water affected the vision of the early tetrapods.
A model of Tiktaalik roseae, a 375-million-year-old transitional fossil that had a neck — unheard of for a fish — and both lungs and gills.
“Both approaches bring something unique, so they should go hand in hand,” Schmitz said. “If I had done the [eye socket size] analysis just by itself, I would be lacking what it could actually mean. Eyes do get bigger, but why?” Sensory modeling can answer this kind of question in a quantitative, rather than qualitative, way.
Schmitz plans to examine other water-to-land transitions in the fossil record — not just that of the early tetrapods — to see if he can find a corresponding increase in eye size. “If you look at other transitions between water and land, and land back to water, you see similar patterns that would potentially corroborate this hypothesis,” he said. For example, the fossil record for marine reptiles, which rely heavily on vision, should also show evidence for an increase in eye socket size as they moved from water to land.
New Ways of Thinking
MacIver’s background as a neuroscientist inevitably led him to ponder how all this might have influenced the behavior and cognition of tetrapods during the water-to-land transition. For instance, if you live and hunt in the water, your limited vision range — roughly one body length ahead — means you operate primarily in what MacIver terms the “reactive mode”: You have just a few milliseconds (equivalent to a few cycle times of a neuron in the brain) to react. “Everything is coming at you in a just-in-time fashion,” he said. “You can either eat or be eaten, and you’d better make that decision quickly.”
But for a land-based animal, being able to see farther means you have much more time to assess the situation and strategize to choose the best course of action, whether you are predator or prey. According to MacIver, it’s likely the first land animals started out hunting for land-based prey reactively, but over time, those that could move beyond reactive mode and think strategically would have had a greater evolutionary advantage. “Now you need to contemplate multiple futures and quickly decide between them,” MacIver said. “That’s mental time travel, or prospective cognition, and it’s a really important feature of our own cognitive abilities.”
That said, other senses also likely played a role in the development of more advanced cognition. “It’s extremely interesting, but I don’t think the ability to plan suddenly arose only with vision,” said Barbara Finlay, an evolutionary neuroscientist at Cornell University. As an example, she pointed to how salmon rely on olfactory pathways to migrate upstream.
Hutchinson agrees that it would be useful to consider how the many sensory changes over that critical transition period fit together, rather than studying vision alone. For instance, “we know smell and taste were originally coupled in the aquatic environment and then became separated,” he said. “Whereas hearing changed a lot from the aquatic to the terrestrial environment with the evolution of a proper external ear and other features.”
The work has implications for the future evolution of human cognition. Perhaps one day we will be able to take the next evolutionary leap by overcoming what MacIver jokingly calls the “paleoneurobiology of human stupidity.” Human beings can grasp the ramifications of short-term threats, but long-term planning — such as mitigating the effects of climate change — is more difficult for us to process. “Maybe some of our limitations in strategic thinking come back to the way in which different environments favor the ability to plan,” he said. “We can’t think on geologic time scales.” He hopes this kind of work with the fossil record can help identify our own cognitive blind spots. “If we can do that, we can think about ways of getting around those blind spots.”
This article was originally published in Quanta Magazine.
Saturday Morning Breakfast Cereal - Biology
.png)
Click here to go see the bonus panel!
Hovertext:
Nah, just kidding, biologists sit in offices filling out grant applications and surveys.
New comic!
Today's News:
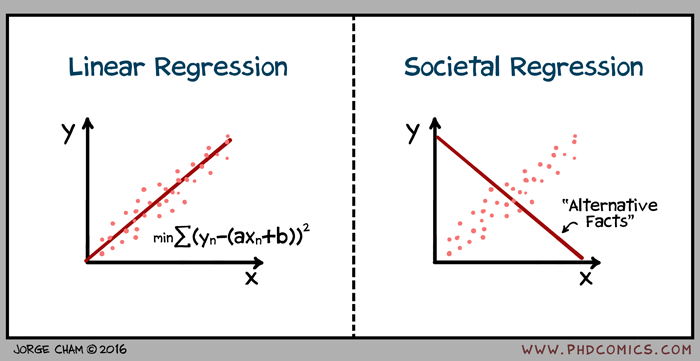
02/06/17 PHD comic: 'Regression'
| Piled Higher & Deeper by Jorge Cham |
www.phdcomics.com
|
|
 |
||
|
title:
"Regression" - originally published
2/6/2017
For the latest news in PHD Comics, CLICK HERE! |
||
Saturday Morning Breakfast Cereal - Sui Generis

Click here to go see the bonus panel!
Hovertext:
Today's comic featuring a young Ernest Becker.
New comic!
Today's News:
Saturday Morning Breakfast Cereal - Math Puzzles
.png)
Click here to go see the bonus panel!
Hovertext:
You come to a mysterious island where everyone always tells the truth...
New comic!
Today's News:
The Heng Balance Lamp Illuminates with a Suspended Magnetic Switch

Seeking a novel way to redesign a light switch while simultaneously retaining a functional and aesthetically pleasing object was the design challenge for Netherlands-based designer Arthur Limpens of Allocacoc DesignNest. His solution was the Heng Balance Lamp, a fun desktop light that relies on a pair of magnets suspended on strings to pull an internal switch. The design concept won a Red Dot Design Award last year, and Allocacoc is now lauching an edition of the lamp through Kickstarter.



Saturday Morning Breakfast Cereal - Perception of Time

Click here to go see the bonus panel!
Hovertext:
FIGHT ME, INTERNET
New comic!
Today's News:
Just two days left to submit a proposal for BAHFest London!
Emails
Artnemiz1Este soy yo por los ultimos 6 o 7 anios

Saturday Morning Breakfast Cereal - Monty Hall Problems

Click here to go see the bonus panel!
Hovertext:
Actually, pretty much everything beyond intro calculus is run by goblins.
New comic!
Today's News:
























