In the Hindu-Buddhist civilizational sphere, the number 108 is among the most sacred and appears as the true or fictitious cardinal number of all manner of philosophical sets and religious series. What makes this number so special? We will try to position ourselves as best as possible into the minds of profundity-oriented symbolists in order to extract their kind of meaning from this unusual number.
Insufficient reasons
Since matters of religious symbolism typically attract self-styled esotericists who have a dislike for serious logical ratiocination, the usual explanations of the sacred status of the number 108 don’t amount to much. Just as those people “explain” the status of the number 12 by merely enumerating “the 12 months, the 12 apostles” etc., they will merely enumerate a number of instances where the number 108 is in evidence.
Thus, I have seen it claimed by Western esotericists that 108 = 6² + 6² + 6², the sum of the squares of the three equal numerals making up the Biblical-Apocalyptic “number of the Beast”, 666. The calculation isn’t incorrect, but it remains unclear why squares should be counted, or why 666 should be of any importance. This number has some strange numerical properties in its own right, but they are not the reason for its popularity among the mystery-minded. The real reason is that through a numerical-alphabetical manipulation best known by its kabbalistic name
gematria, the number refers to a Roman emperor disliked by the first Christians who called him “the Beast”. Emperor or “Caesar” seems to be the meaning of the component 60, this being the numerical value of the Greek letter Ksi, shorthand for its Greek rendering
Kaisar. This probably doesn’t refer to Nero, as has been assumed for long, but to “Divus Claudius”, the 6th emperor, who came after Julius Caesar, Octavian August, Tiberius, Germanicus (who received the
imperium maius but was murdered; his caesarian status is shown by the fact that the succession devolved to his son:), Caligula. Even Claudius’ mother considered Claudius ugly like a beast, and his initials DC were read in Latin as the number 500 + 100 = 600. So, probably 666 means “the 6
th Caesar/60, named D.C./600”.
Admittedly, there are other explanations, but whatever the details, the reference to “the number of the Beast” is merely an expression of the abysmal hatred of Rome by some early Christians, a mere footnote in history. At any rate, the abusive religio-political slogan “666” is totally irrelevant to any serious philosophy. It is equally irrelevant to Hindu-Buddhist culture, and relating it to the status of 108 is anachronistic since it appeared on the scene centuries
after the number 108 gained its aura of sacredness.
Even where the explainers try to prove their point with proper Hindu-Buddhist examples, they fail to get to the bottom of the matter. Thus, the Upanishads (philosophical texts completing the Vedic corpus) are classically counted as 108, eventhough their actual number, depending on which ones you include, can range from 13 to more than 200. Rosaries east of the Indus have 108 beads, the Nepalese parliament has 108 seats. The poses of
Bhârata Natyam dancing, the number of
gopî-s (cowgirls) enamoured of Krishna, the number of sacred sites in the tradition of Vishnu worship, the number of Buddhist
arhat-s (realized saints), and many other sacred sets are all conventionally counted as 108. Likewise with derived numbers, e.g. the Rg-Vedic verses are conventionally counted as very approximately 10800, the
Purâna-s as 18, the
Bhagavad-Gîtâ has 18 chapters, and many Hindu monks carry titles like
“Swâmi 1008 Padmânanda”.
All very fine, but that list doesn’t
explainanything. The number 108 has been chosen in these instances, and often forced upon rather unwilling sets as their cardinal number, because it was already a sacred number to begin with. We need something more objective as a basis for the special status of this number.
Among attempts to find a more solid basis, we still have to be wary of cheap and easy proposals. Thus, I have seen it claimed that “108 x 20 = 2160, the number of years spent by the equinox in each Zodiac sector”, on the assumption that the total precessional cycle takes 2160 x 12 years, i.e. 25,920 years or neatly 1° per 72 years (and the extra assumption that the Vedic seers knew and cared about the precessional cycle). But in reality, the cycle takes ca. 25,791 years, which doesn’t yield any round number when divided by 108.
It is already better to note that 108 lurks in a corner of the Hindu (or actually Indo-European) number 432 with any number of zeroes added. Thus, 432,000, the number of years sometimes attributed to a
Yuga, a world age, which happens to be equal to the number of guardians of the Germanic
Walhalla or heaven (viz. 800 for every one of its 540 gates), can be analysed as 108 x 4000. Or as 18 x 24000, for that matter. This is true, but is it important? Many numbers are related to other numbers. Is it relevant to anything?
So, we will try to do better than that and give correct data which underlie the special status of our sacred number in a more compelling manner. We will distinguish between a pair of contingent astronomical facts singling out the number 108 and four mathematical properties of the number 108, two of these conditional and two unconditional.
Solar and lunar distances
It could have been otherwise, but it so happens that the distance between the earth and the sun equals about 108 (actually 107-odd) times the sun’s diameter. Likewise, it so happens that the distance between the earth and the moon equals about 108 (actually 109-odd) times the moon’s diameter. That sun and moon look equally big in the earthly sky is the immediate result of their having the same ratio between distance and diameter. Moreover, it so happens that the sun’s diameter approximately equals 108 times the earth’s diameter.
These are contingent data, which means that they could have been different. And they are subject to change, meaning that if you look deep enough into the past or the future, you find values considerably different from the present ones of ca. 108. While the distance between the sun and its planets is fairly stable, the distance between the earth and the moon is subject to steady and ultimately very sizable changes. In the times of the dinosaurs, the moon was so close to the earth that a lunar revolution (i.e. a month) took only a few earthly days, with the days themselves also being shorter than today. In the future, the lunar revolution will take thirty days, forty days, etc. Its distance from the earth will then equal 110 lunar diameters, 120 etc.
It is a cosmic stroke of luck that the solar and lunar distances happen to match the number 108, a remarkable number for non-contingent reasons we will discuss below, right at the time when life on earth was reaching a level of intelligence sufficient to start astronomical observations and wonder at this coincidence. Just as it is a cosmic stroke of luck that in this same age, the moon is at such a distance from the earth that its annual number of revolutions is approximately 12, another number with unique non-contingent properties.
Can we be sure that this remarkable astronomical state of affairs has played a role in the selection of 108 as a sacred number? Did the ancient Indians know about the moon’s diameter or its distance from the earth? According to Richard L. Thompson (
Mysteries of the Sacred Universe, Govardhan Hill Publ. 2000, p.16, p.76), the medieval
Sûrya-Siddhânta gives an unrealistically small estimate for the distance earth-sun, but the estimate for the distance earth-moon and the lunar diameter differs less than 10% from the modern value. The ratio between distance and diameter of the moon is implicitly given there as 107.5, admittedly a very good approximation.
However, I have never heard of any text, whether from the Vedic or the medieval period, that explicitly derives the importance of the number 108 from these or any other astronomical data. But this is merely an argument from silence, with limited proof value. For on the other hand, the estimation of the relative distance of sun or moon isn’t that difficult to calculate even without any instruments: “Take a pole, mark its height, and then remove it to a place 108 times its height. The pole will look exactly of the same angular size as the moon or the sun.” (Subhash Kak: “Shri 108 and Other Mysteries”,
Sulekha.com, 27 Nov. 2001) Also, in some respects the Vedic-age astronomers were more advanced than their medieval successors, who had jettisoned part of their own tradition in favour of Hellenistic import.
So, it remains speculative but quite possible that the solar and lunar data were estimated with a good degree of accuracy at the time when 108 was selected as a sacred number. But it is also possible that the selection was made purely on the basis of the non-astronomical considerations discussed in the following sections.
One of the arithmetical properties of 108 is dependent on the choice of counting system. In the near-universally used decimal counting system, the quantity 108 is expressed as “108”, meaning “1 hundred, 0 tens, 8 units”. In other counting systems, it would look different, e.g. in a duodecimal (12-based) system, it would be written as “90”, and in the binary system, it is written as “1101100”. Assuming the conventional decimal system, what is remarkable about “1-0-8”?
Like 18, it brings together the numerals 1 and 8, with the former in the leading and the latter in the lowly position. The main difference (valid even more in subsequent numbers like 1008) is merely that an abyss of worshipful distance is created between the regal 1 and the servile 8. So, let us briefly focus on this symbolism of 1 and 8. It is chiefly remarkable as a reference to yet other important symbols.
In the magic square of 9, there is 1 little square in the middle and 8 on the periphery. Also, the 1 central number is 5, the sum of the 8 peripheral numbers is 40, yielding a ratio of 1:8. The magic square itself, with equal sums of the three numerals on every line, is an important symbol of cosmic order, balance and integration. Painted on walls or wrought into little metal plates it is used as a luck-charm.
Moreover, consider the sums in the magic square, adding the central number and a number in the middle of the sides, yielding the number in an adjoining corner (counting only the units): 5 + 1 = 6; 5 + 7 = 2 (12 modulo 10, as it were); 5 + 9 = 4 (14 modulo 10); 5 + 3 = 8. If you draw lines following the numerals in these sums, you get the
Swastika, yet another lucky symbol in Hindu-Buddhist culture.
The “nine planets” of Hindu astronomy are also often depicted in a square arrangement for ritual purposes such as the
Navagraha Agnihotra (nine-planet fire ceremony), with the sun in the middle and the 8 others around it: moon, Mercury, Venus, Mars, Jupiter, Saturn,
Râhu (northward intersection of lunar orbit and ecliptic, “Dragon’s head”) and
Ketu (southward intersection, “Dragon’s tail”). So, 18 or 108 may add some detail to the symbolism of 9 as representing the planets. This is, however, of lesser importance than the magic square because the number of planets is contingent and changeable whereas mathematical properties are intrinsic and forever.
The Golden Section and 108°
A conditional geometrical property of 108 is dependent on the conventional division of the circle into 360°. This division is arithmetically very practical, it also alludes to the division of the year in ca. 365 days, it is now universally accepted, yet it is contingent and essentially only the result of a human convention. At least one alternative division is known, viz. the division into 400° introduced during the French Revolution on the assumption that the division into religion-tainted numbers like 7 and 360 was less “rational” than the division into 10 or 100 or their multiples. Hence also the Revolutionary replacement of the 7-day week by a 10-day week and the definitional choice of the meter as one hundred-thousandth of one “decimal degree” measured on the earth’s equator of 40,000 km.
But for now, we may settle for the division in 360°. In that case, the angle of 108° has a unique property: the ratio between the straight line uniting two points at 108° from each other on a circle’s circumference (in effect one of the sides of a 10-pointed star) and the radius of that circle equals the Golden Section. Likewise, the inside of every angle of a pentagon measures 108°, and the pentagon is a veritable embodiment of the Golden Section, e.g. the ratio between a side of the 5-pointed star and a side of the pentagon is the Golden Section. So, there is an intimate link between the number 108 and the Golden Section. But why should this be important?
The Golden Section means a proportion between two magnitudes, the major and the minor, such that the minor is to the major as the major is to the whole, i.e. to the sum of minor and major. The general equation yielding the Golden Section is A/B = (A + B)/A, or alternatively but equivalently, X = 1 + 1/X. In numbers, X = (1 + square root 5)/2; or decimally, X = 1, 618… This infinite series of decimals can be replaced with a more predictable infinite series of numbers, viz. X equals the limit of the series G/F in which F is any member and G is the very next member of the Fibonacci series, i.e. the series in which every member equals the sum of the two preceding members: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,… This means that every next fraction G/F, i.e. 1/1, 2/1, 3/2, 5/3, 8/5 etc. forms a better approximation of the Golden Section, whose value can be approximated to any desired degree of precision if fractions of sufficiently highly-placed members of the Fibonacci series are considered.
In art and architecture, it is found that the Golden Proportion is naturally pleasing to our inborn tastes. In living nature, there are plenty of sequences where every member stands to the preceding member in a Golden Proportion or its derivatives (square root etc.), e.g. the distances between or the sizes of the successive twigs growing on a branch, the layers of petals on a flower, the rings of a conch, the generations of a multiplying rabbit population, etc. What this symbolizes is the law of invariance: in every stage of a development, the same pattern repeats itself. The son is to the father as the father was to the grandfather. Wheels within wheels: every whole consisting of parts is itself likewise part of a larger whole. And the principle of order: the underling obeys the orders of his master to the same extent that the master obeys the requirements of the whole. Or with a pre-feminist maxim: “he for God alone, she for God in him”, i.e. the wife serves the husband because (and to the extent that) the husband serves the cosmic order defining his duties. As Confucius said, the authority of the ruler, his capability of making the people willingly obey him, is that he himself obeys the Laws of Heaven.
So, the Golden Section is a meaningful symbol in the cosmological, aesthetical and ethical realms. And somewhere in a corner of Golden Section lore, in the pentagon and decagon, we see the number 108 participating. This is meritorious though perhaps a bit too indirect to count as sensational.
An intrinsic and ever-unchangeable property of 108 is that it equals 9 times 12, the product of two smaller sacred numbers. It is the number of divisions in the Zodiac in the so-called
Navamsha horoscope, a horoscope which Hindu astrologers always calculate along with the basic horoscope, and in which all original positions expressed in angular distance from the beginning point of the Zodiac are multiplied by 9. This implies, for example, that a planet at 8° Aries is projected to 72°, meaning 12° Gemini. In effect, the whole sector between 6°40’ and 10° Aries is projected onto Gemini (i.e. between 60° and 90°) and given a Gemini colouring, just as the sector between 10° and 13°20 Aries is
navamsha-projected onto Cancer, etc. This way, every one of the 12 signs is subdivided into 9 sectors, or 108 in total. But of course, this doesn’t explain the status of 108, as the idea of subdividing the Zodiac this way apparently results from the awe in which 108 or 9 x 12 was already held.
As we have seen, 9 is the Hindu number of planets, and 12 is the Zodiac, so 108 is the total number of planet-in-Zodiacal-sign combinations. This makes it into the total set of all possible planetary influences taken separately, or in a more generalized symbolism, the matrix containing all possibilities. However, to purists, 9 as the number of planets isn’t good enough. For one thing, the Hindu definition of a planet is pre-heliocentric, counting sun and moon and their two eclipse points as planets all while failing to count the earth as a planet (though it so happens that planets by the modern astronomical definition are again counted as 9, from Mercury to Pluto including the earth). Also, planets may be added through empirical discovery, as some have indeed been in astronomy and in Western astrology; and in some rare but not-impossible catastrophe, a planet may disappear. They are only creatures, born from dust and returning to dust. If we’re looking for intrinsic properties of numbers, we should not settle for contingent data such as the present number of Hindu “planets”.
To the unique properties of 12, revealing it to be a logical symbol of cosmic order, we have devoted a separate paper,
Why Twelve?, where we have focused on its unconditional properties, both arithmetical and geometrical. We may add that, conditional upon the choice of the decimal system, 12 is structured as 1 tenfold plus 2 units: 1 big, 2 small. Which to a freely-associating symbolist mind can mean: 1 precedes 2 (as indeed it does, in fact it is the most elementary observation to be made in the number series, e.g. long preceding the realization that there must be a zero), unity is superior to division, oneness precedes and underlies polarity, the odd/
yang dominates the even/
yin. Note however that for all their inequality, the numbers 1 and 2 and all that they symbolize are at any rate
united and synthesized in the number 12 and in whatever the latter symbolizes. Meanwhile, this conditional arithmetical property of 12 must remain inferior to the unconditional properties of 12, especially those of 12 conceived geometrically as the regular dodecagon, e.g. the fact that its construction uniquely flows automatically from the construction of the circle, keeping the same compass width; and the fact that it bridges the gap between straight/radius and round/circumference by dividing both rationally in a single move (the radius into 2, the quarter-circumference into 3).
Like 12, the number 9 has its unusual properties. Once more, we cannot be satisfied with simply enumerating instances where 9 has been used in a sacred context: the 9 worlds of Germanic cosmology, the 9 Muses, etc. We want objective properties, and when looking for these, we must again distinguish between conditional and unconditional properties. Thus, it is often remarked that 9 is the highest among the decimal numerals, and hence symbolizes anything that is highest, including God, who, in comparison with anything you may propose, is always Greater. However, this property is conditional upon our choice of numeral system, i.c. decimal rather than binary or any other: in the binary system, the number 1 would have this property, and in the duodecimal one, the number eleven would. Likewise, 9’s property of equalling the sum of the numerals in its own multiples (e.g. in 9 x 8 = 72, we find that 7 + 2 = 9) is again dependent on our choice of the decimal system.
For unconditional properties, we might look at some characteristics of the enneagon (9 x 40°). This is the first polygon with a non-prime base (as distinct from the heptagon, 7 being a prime number) that eludes construction with ruler and compass. This contrasts sharply with the division of the circle into 4 or 6 or 12, which is so simple and natural, or with its division into 5 or 10, which is more complicated but very rewarding (yielding the Golden Section) and at any rate possible. So, 9, though analysable as 3 x 3, is elusive. Does anyone care to read some symbolism into this property? If 7 represents the mystical eluding the rational, what should be represented by 9, which is more structured yet equally eludes rational construction? Let’s see: how about God, who always eludes our concepts?
Allahu Akbar, God is greater!
But we need not look that far. Whatever else 9 may be, its most immediate arithmetical property is certainly that it equals 3², or 3 x 3. Unlike the neat balance of even numbers like 2 or 4, suggesting stability and a waiting matrix of potentialities, the number 3 expresses motion, as even the most vulgar book on number symbolism will tell you. The number 9, therefore, is a movement affecting the movement, i.e. acceleration. It is dynamic par excellence, Shakti as the dynamic expression of static Shiva. The primal form of acceleration is the change from rest to motion, i.e. setting things in motion, starting the whole process from zero. This, of course, is the doing of the Creator who is Greater. Or as the Scholastics used to say: God is not Potency, God is pure Act.
So, whereas 12 represents synthesis of opposites within an ordered cosmos (3 x 4, time-space, motion-structure) and harmonization of self and non-self, 9 represents unfettered dynamism, pure self-expression riding roughshod over the non-self, the joy of being entirely oneself. It transcends and leaves behind all compromise in favour of purity and absorption. Its structure as 3 x 3 actually explains its elusiveness: whereas divisions of any angle into 2 and its multiples are always feasible and simple, the division into 3 is impossible, though very good approximative techniques have been developed. Even folding a letter into three requires a manual jump, an approximation rather than a slow but sure technique guaranteeing an exact division into equal parts. The enneagon is the first regular polygon which requires for its construction the
trisectionof a known angle (120°, itself easily constructed though not by trisecting the “angle” of 360°), an impossible operation with ruler and compass. Likewise, according to poets, the Absolute cannot be caught in a conceptual net but can only be approximated, hinted at, spoken of in parables and metaphors.
Let’s put ourselves into the mood of god-seekers in order to understand this. As 9 x 12, the number 108 infuses the cosmic order represented by 12 with the god-drunkenness, the enthusiasm free of all doubts, the pure dedication represented by 9. That makes it an excellent number for the prayer-wheel or rosary, which is used in a disciplined and systematic manner in order to lift up the spirit towards god-absorption.
Among other intrinsic and ever-unchangeable properties, it may be hard to choose which one is sufficiently relevant. Thus, 108 equals the sum of the first 9 multiples of 3, viz. 0, 3, 6, 9, 12, 15, 18, 21 and 24. This reconfirms its intimate relation with the richly symbolic number 9, but then, so what?
Slightly more remarkable is that 108 equals the product of the second power of 2 and the third power of 3, i.e. the first non-trivial even and odd numbers multiplied by themselves as many times as themselves. In figures: 108 = 2² x 3³, or 108 = 2 x 2 x 3 x 3 x 3. This way, it unites on their own terms the polar opposites of even and odd, the numerical counterparts of female and male, yin and yang, etc. If nothing else, at least it’s cute, is it not? That may well be the most we can expect of number symbolism.
(copyright: author, October 2003)
(in case we have missed some important symbolically-charged properties of the number 108, we welcome feedback)
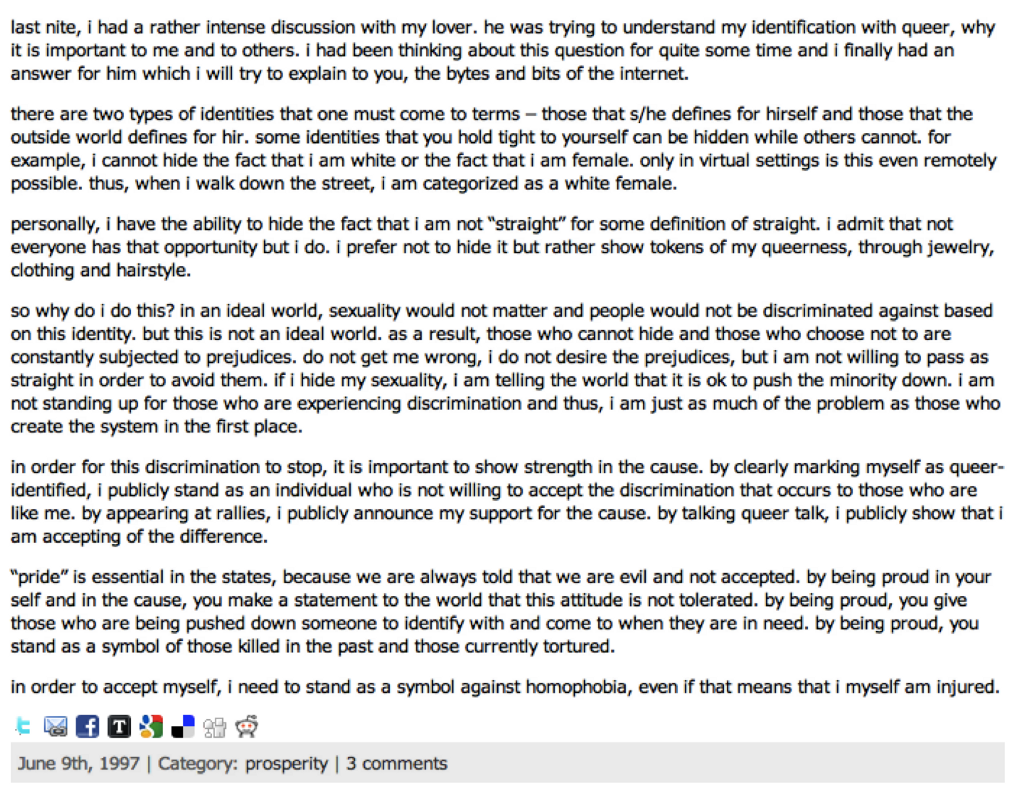I started blogging in 1997. I was 19 years old. I didn’t call it blogging then, and my blog didn’t look like it does now. It was a manually-created HTML site with a calendar made of tables (OMG tables) and Geocities-style forward and back buttons with terrible graphics. I posted entries a few times a week as part of an independent study on Buddhism as a Brown University student that involved both meditation and self-reflection. Each week, the monk I was working with would ask me to reflect on certain things, and I would write. And write. And write. He lived in Ohio and had originally proposed sending letters, but I thought pencils were a foreign concept. I decided to type my thoughts and that, if I was going to type them, I might as well put them up online. Ah, teen logic.
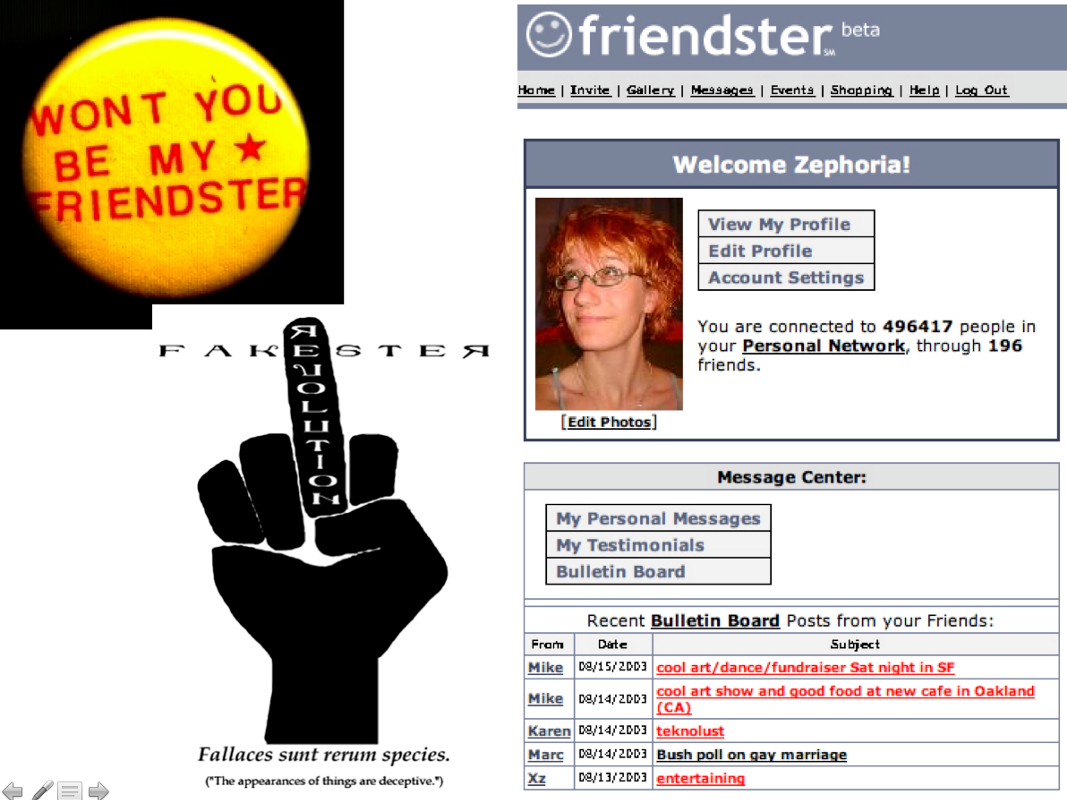As research became more central to my life, my blog became more focused on my research. In December 2002, I started tracking Friendster. (Keep in mind that the first public news story was written about Friendster by the Village Voice in June of 2003.) I was documenting my understanding of the new technologies that were emerging because that’s what I was thinking about. But because I was writing about tech, my blog caught the eye of technology folks who were trying to track this new phenomenon.
My experience with objectification took on a whole new level in 2009 when, at Web2.0 Expo, my experience on stage devolved. I wrote about this incident in gory detail on my blog, but the basic story is that I talk fast. And when I’m nervous, I talk even faster. I was nervous, it was a big stage, there were high-power lights so I couldn’t see anything. And there was a Twitter feed behind me that I couldn’t see. As I nervously started in on my talk, the audience began critiquing me on Twitter and then laughing at what others wrote. It devolved into outright misogyny—the Twitter stream was taken down and then put back up. The audience was loud but clearly not listening to what I had to say. I didn’t know what was going on, and I melted. I talked faster, I stared at the podium. I didn’t leave stage in tears, but I thought about doing so. It was humiliating.
) said:
