在这篇文章中,我会向大家展示一些排序算法的可视化过程。我还写了一个工具,大家可对比查看某两种排序算法。
引言
首先,我认为是最重要的是要理解什么是“排序算法”。根据维基百科,排序算法(Sorting algorithm)是一种能将一串数据依照特定排序方式进行排列的一种算法。最常用到的排序方式是数值顺序以及字典顺序。有效的排序算法在一些算法(例如搜索算法与合并算法)中是重要的,如此这些算法才能得到正确解答。排序算法也用在处理文字数据以及产生人类可读的输出结果。
接下来,我会说明一些算法。所有算法皆由C#代码实现,大部分的算法思想都可以在维基百科上找到。 所呈现的算法有:
- 双向冒泡排序
- 冒泡排序
- 桶排序
- 梳排序
- 循环排序
- 地精排序
- 堆排序
- 插入排序
- 归并排序
- 奇偶排序
- 鸽笼排序
- 快速排序
- 使用冒泡的快排
- 选择排序
- 希尔排序
我已经决定要创建GUI可视化的排序算法。该项目还允许用户保存为GIF图像及设置动画输出排序速度。
使用代码
该解决方案由两个项目组成。第一个项目称为组件提供的创建GIF动画图像类。该项目是基于NGIF项目的。关于这个项目的更多信息可以在这里找到。
第二个项目可以称为排序比较,它是解决方案的主要组成部分。其中,通过一个名为frmMain的结构可以选择排序算法,设置你想要排序,排序的速度,排序数量,并选择是否要创建动态图片。在窗体上放置两个面板称为pnlSort1和pnlSort2,其中分拣可视化的呈现方式。
每个算法都都通过自己的排序方式进行命名,并接受一个IList参数,并返回一个IList对象。
DrawSamples方法可以在面板上进行绘图。产生的随机样本之后就会调用它。通过点击随机按钮生成的样本会保存在数组中。
private void DrawSamples()
{
g.Clear(Color.White);
for (int i = 0; i < array.Count; i++)
{
int x = (int)(((double)pnlSamples.Width / array.Count) * i);
Pen pen = new Pen(Color.Black);
g.DrawLine(pen, new Point(x, pnlSamples.Height),
new Point(x, (int)(pnlSamples.Height - (int)array[i])));
}
}
该方法随机产生数据放于数组中。
public void Randomize(IList list)
{
for (int i = list.Count - 1; i > 0; i--)
{
int swapIndex = rng.Next(i + 1);
if (swapIndex != i)
{
object tmp = list[swapIndex];
list[swapIndex] = list[i];
list[i] = tmp;
}
}
}
在排序过程中,当复选框创建的动画被选中,数组中两个数交换的话就会产生图像。此图像索引从0到n,其中n代表交换的次数。
private void SavePicture()
{
ImageCodecInfo myImageCodecInfo = this.getEncoderInfo("image/gif");
EncoderParameter myEncoderParameter = new EncoderParameter(
System.Drawing.Imaging.Encoder.Compression, (long)EncoderValue.CompressionLZW);
EncoderParameter qualityParam =
new EncoderParameter(System.Drawing.Imaging.Encoder.Quality, 0L);
EncoderParameters myEncoderParameters = new EncoderParameters(1);
EncoderParameters encoderParams = new EncoderParameters(2);
encoderParams.Param[0] = qualityParam;
encoderParams.Param[1] = myEncoderParameter;
string destPath =
System.IO.Path.Combine(txtOutputFolder.Text, imgCount + ".gif");
bmpsave.Save(destPath, myImageCodecInfo, encoderParams);
imgCount++;
}
排序算法
冒泡排序

冒泡排序也被称为下沉排序,是一个简单的排序算法,通过多次重复比较每对相邻的元素,并按规定的顺序交换他们,最终把数列进行排好序。一直重复下去,直到结束。该算法得名于较小元素“气泡”会“浮到”列表顶部。由于只使用了比较操作,所以这是一个比较排序。
冒泡排序算法的运作如下:
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
由于它的简洁,冒泡排序通常被用来对于程序设计入门的学生介绍算法的概念。但同样简单的插入排序比冒泡排序性能更好,所以有些人认为不需要再教冒泡排序了。
public IList BubbleSort(IList arrayToSort)
{
int n = arrayToSort.Count - 1;
for (int i = 0; i < n; i++)
{
for (int j = n; j > i; j--)
{
if (((IComparable)arrayToSort[j - 1]).CompareTo(arrayToSort[j]) > 0)
{
object temp = arrayToSort[j - 1];
arrayToSort[j - 1] = arrayToSort[j];
arrayToSort[j] = temp;
RedrawItem(j);
RedrawItem(j - 1);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
}
}
}
return arrayToSort;
}
| Worst case performance: | O(n2) |
| Best case performance: | O(n) |
| Average case performance: | O(n2) |
| Worst case space complexity: | O(1) auxiliary |
双向冒泡排序

鸡尾酒排序,也称为双向冒泡排序、调酒器排序、搅拌排序(可以参考选择排序的一个变种)、纹波排序、接送排序,或欢乐时光排序。它由冒泡排序变化而来,是一种稳定的比较排序算法。该算法不同于冒泡排序,它在排序上由两个方向同时进行。该排序算法只是比冒泡排序稍难实现,但解决了冒泡排序中的“乌龟问题”(数组尾部的小值)。
首先从左向右方向为大元素移动方向,从右向左方向为小元素移动方向,然后每个元素都依次执行。在第 i 次移动后,前 i 个元素和后个 i 元素都放到了正确的位置,也不需要在检查一次。每次缩短已排序的那部分列表,都可以减半操作次数。
但是在乱数序列的状态下,双向冒泡排序与冒泡排序的效率都很差劲。
public IList BiDerectionalBubleSort(IList arrayToSort)
{
int limit = arrayToSort.Count;
int st = -1;
bool swapped = false;
do
{
swapped = false;
st++;
limit--;
for (int j = st; j < limit; j++)
{
if (((IComparable)arrayToSort[j]).CompareTo(arrayToSort[j + 1]) > 0)
{
object temp = arrayToSort[j];
arrayToSort[j] = arrayToSort[j + 1];
arrayToSort[j + 1] = temp;
swapped = true;
RedrawItem(j);
RedrawItem(j + 1);
pnlSamples.Refresh();
if(chkCreateAnimation.Checked)
SavePicture();
}
}
for (int j = limit - 1; j >= st; j--)
{
if (((IComparable)arrayToSort[j]).CompareTo(arrayToSort[j + 1]) > 0)
{
object temp = arrayToSort[j];
arrayToSort[j] = arrayToSort[j + 1];
arrayToSort[j + 1] = temp;
swapped = true;
RedrawItem(j);
RedrawItem(j + 1);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
}
}
} while (st < limit && swapped);
return arrayToSort;
}
| Worst case performance: | O(n2) |
| Best case performance: | O(n) |
| Average case performance: | O(n2) |
| Worst case space complexity: | O(1) auxiliary |
桶排序
桶排序,或称为箱排序,是一种把数列划分成若干个桶的排序算法。在每个桶内各自排序,或者使用不同的排序算法,或通过递归方式继续使用桶排序算法。这是一个分布排序,是最能体现出数字意义的一种基数排序。桶排序是鸽巢排序的一种归纳结果。当要被排序的数组内的数值是均匀分配的时候,桶排序使用线性时间(Θ(n))。但桶排序并不是 比较排序,他不受到 O(n log n) 下限的影响。
桶排序的流程:
- 设置一个定量的数组当作空桶子。
- 寻访串行,并且把项目一个一个放到对应的桶子去。
- 对每个不是空的桶子进行排序。
- 从不是空的桶子里把项目再放回原来的串行中。
public IList BucketSort(IList arrayToSort)
{
if (arrayToSort == null || arrayToSort.Count == 0) return arrayToSort;
object max = arrayToSort[0];
object min = arrayToSort[0];
for (int i = 0; i 0)
{
max = arrayToSort[i];
}
if (((IComparable)arrayToSort[i]).CompareTo(min) < 0)
{
min = arrayToSort[i];
}
}
ArrayList[] holder = new ArrayList[(int)max - (int)min + 1];
for (int i = 0; i < holder.Length; i++)
{
holder[i] = new ArrayList();
}
for (int i = 0; i < arrayToSort.Count; i++)
{
holder[(int)arrayToSort[i] - (int)min].Add(arrayToSort[i]);
}
int k = 0;
for (int i = 0; i 0)
{
for (int j = 0; j < holder[i].Count; j++)
{
arrayToSort[k] = holder[i][j];
RedrawItem(k);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
k++;
}
}
}
return arrayToSort;
}
| Worst case performance: | O(n2.k) |
| Best case performance: | - |
| Average case performance: | O(n.k) |
| Worst case space complexity: | O(n.k) |
梳排序

梳排序是一个相对简单的排序算法,最初它由Wlodzimierz Dobosiewicz于1980年设计出来。后来由斯蒂芬和理查德重新发现和推广。他们的文章在1991年4月发表在字节杂志上。梳排序改善了冒泡排序和类似快速排序的竞争算法。其要旨在于消除乌龟,亦即在阵列尾部的小数值,这些数值是造成冒泡排序缓慢的主因。相对地,兔子,亦即在阵列前端的大数值,不影响冒泡排序的效能。
在冒泡排序中,任何两个元素进行比较时,他们总是距离彼此为1。梳排序的基本思想是可以不是1。
梳排序中,开始时的间距设定为列表长度,然后每一次都会除以损耗因子(一般为1.3)。必要的时候,间距可以四舍五入,不断重复,直到间距变为1。然后间距就保持为1,并排完整个数列。最后阶段就相当于一个冒泡排序,但此时大多数乌龟已经处理掉,此时的冒泡排序就高效了。
public IList CombSort(IList arrayToSort)
{
int gap = arrayToSort.Count;
int swaps = 0;
do
{
gap = (int)(gap / 1.247330950103979);
if (gap 0)
{
object temp = arrayToSort[i];
arrayToSort[i] = arrayToSort[i + gap];
arrayToSort[i + gap] = temp;
RedrawItem(i);
RedrawItem(i + gap);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
swaps = 1;
}
i++;
} while (!(i + gap >= arrayToSort.Count));
} while (!(gap == 1 && swaps == 0));
return arrayToSort;
}
| Worst case performance: | - |
| Best case performance: | - |
| Average case performance: | - |
| Worst case space complexity: | O(1) |
圈排序

Cycle sort is an in-place, unstable sorting algorithm, a comparison sort that is theoretically optimal in terms of the total number of writes to the original array, unlike any other in-place sorting algorithm. It is based on the idea that the permutation to be sorted can be factored into cycles, which can individually be rotated to give a sorted result.
Unlike nearly every other sort, items are never written elsewhere in the array simply to push them out of the way of the action. Each value is either written zero times, if it’s already in its correct position, or written one time to its correct position. This matches the minimal number of overwrites required for a completed in-place sort.
它是一个就地、不稳定的排序算法,根据原始的数组,一种理论上最优的比较,并且与其它就地排序算法不同。它的思想是把要排的数列分解为圈,即可以分别旋转得到排序结果。
不同于其它排序的是,元素不会被放入数组的中任意位置从而推动排序。每个值如果它已经在其正确的位置则不动,否则只需要写一次即可。也就是说仅仅最小覆盖就能完成排序。
public IList CycleSort(IList arrayToSort)
{
int writes = 0;
for (int cycleStart = 0; cycleStart < arrayToSort.Count; cycleStart++)
{
object item = arrayToSort[cycleStart];
int pos = cycleStart;
do
{
int to = 0;
for (int i = 0; i < arrayToSort.Count; i++)
{
if (i != cycleStart && ((IComparable)arrayToSort[i]).CompareTo(item) < 0)
{
to++;
}
}
if (pos != to)
{
while (pos != to && ((IComparable)item).CompareTo(arrayToSort[to]) == 0)
{
to++;
}
object temp = arrayToSort[to];
arrayToSort[to] = item;
RedrawItem(to);
item = temp;
RedrawItem(cycleStart);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
writes++;
pos = to;
}
} while (cycleStart != pos);
}
return arrayToSort;
}
| Worst case performance: | O(n2) |
| Best case performance: | - |
| Average case performance: | O(n2) |
| Worst case space complexity: | O(1) |
地精排序

地精排序(gnome sorting,大部分地方翻成“侏儒排序”,“地精排序”明明更好听呀,本文就这么用了。)最初由哈米德在2000年的时候提出,当时称为傻瓜排序,之后被迪克说明并且命名为“地精排序”。除了某个元素是经过一系列的互换(类似冒泡排序)才到了它的正确位置之外,它和插入排序挺相似。
它在概念上很简单,不需要嵌套循环。运行时间是O(n2),如果列表基本有序,则时间为O(n)。实际上,它和插入排序一样,平均运行时O(n2)。
The algorithm always finds the first place where two adjacent elements are in the wrong order, and swaps them. It takes advantage of the fact that performing a swap can introduce a new out-of-order adjacent pair only right before or after the two swapped elements. It does not assume that elements forward of the current position are sorted, so it only needs to check the position directly before the swapped elements.
地精算法总是发现第一个 【两个相邻元素存在错误的顺序】,然后把他们交换。原理是,交换一对乱序元素后,会产生一对新的无序相邻元素,而这两个元素要么交换前有序,要么交换后有序。它不认为元素当前的位置是有序的,所以它只需要在交换元素前直接检查位置。
public IList GnomeSort(IList arrayToSort)
{
int pos = 1;
while (pos = 0)
{
pos++;
}
else
{
object temp = arrayToSort[pos];
arrayToSort[pos] = arrayToSort[pos - 1];
RedrawItem(pos);
arrayToSort[pos - 1] = temp;
RedrawItem(pos - 1);
RefreshPanel(pnlSamples);
if (savePicture)
SavePicture();
if (pos > 1)
{
pos--;
}
}
}
return arrayToSort;
}
| Worst case performance: | O(n2) |
| Best case performance: | - |
| Average case performance: | - |
| Worst case space complexity: | O(1) |
堆排序

堆排序是从数据集构建一个数据堆,然后提取最大元素,把它放到部分有序的数组的末尾。提取最大元素后,重新构建新堆,然后又接着提取新堆这的最大元素。重复这个过程,直到堆中没有元素并且数组已排好。堆排序的基本实现需要两个数组:一个用于构建堆,另一个是存放有序的元素。
堆排序把输入数组插入到一个二叉堆的数据结构中。最大值(大根堆)或最小值(小根堆)会被提取出来,直到堆空为止,提取出来的元素,是已经排好序的。每次提取后,堆中没变换的元素依然保留了,所以(堆排序的)唯一消耗就是提取过程。
在提取过程中,所需要的空间,就是用于存放堆的空间。为了实现恒定的空间开销,堆是存储在输入数组中还没有完成排序的那部分空间中。堆排序使用了两个堆操作:插入和根删除。每个提取的元素放到数组的最后一个空位置。数组剩余位置存放待排元素。
public IList HeapSort(IList list)
{
for (int i = (list.Count - 1) / 2; i >= 0; i--)
Adjust(list, i, list.Count - 1);
for (int i = list.Count - 1; i >= 1; i--)
{
object Temp = list[0];
list[0] = list[i];
list[i] = Temp;
RedrawItem(0);
RedrawItem(i);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
Adjust(list, 0, i - 1);
}
return list;
}
public void Adjust(IList list, int i, int m)
{
object Temp = list[i];
int j = i * 2 + 1;
while (j <= m)
{
if (j < m)
if (((IComparable)list[j]).CompareTo(list[j + 1]) < 0)
j = j + 1;
if (((IComparable)Temp).CompareTo(list[j]) < 0)
{
list[i] = list[j];
RedrawItem(i);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
i = j;
j = 2 * i + 1;
}
else
{
j = m + 1;
}
}
list[i] = Temp;
RedrawItem(i);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
}
| Worst case performance: | O(n log n) |
| Best case performance: | O(n log n) |
| Average case performance: | O(n log n) |
| Worst case space complexity: | O(1) |
插入排序

插入排序的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
具体算法描述如下:
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2~5
public IList InsertionSort(IList arrayToSort)
{
for (int i = 1; i < arrayToSort.Count; i++)
{
object val = arrayToSort[i];
int j = i - 1;
bool done = false;
do
{
if (((IComparable)arrayToSort[j]).CompareTo(val) > 0)
{
arrayToSort[j + 1] = arrayToSort[j];
RedrawItem(j + 1);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
j--;
if (j < 0)
{
done = true;
}
}
else
{
done = true;
}
} while (!done);
arrayToSort[j + 1] = val;
RedrawItem(j + 1);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
}
return arrayToSort;
}
| Worst case performance: | O(n2) |
| Best case performance: | O(n) |
| Average case performance: | O(n2) |
| Worst case space complexity: | O(1) |
归并排序

从概念上讲,归并排序的工作原理如下:
- 如果列表的长度是0或1,那么它已经有序。否则:
- 未排序的部分平均划分为两个子序列。
- 每个子序列,递归使用归并排序。
- 合并两个子列表,使之整体有序。
归并排序包含两个主要观点,以改善其运行时:
- 一个小列表排序的花费少于大列表。
- 把两个有序表合并,要比直接排列一个无序表花费更少的步骤。例如,您只需要遍历每个有序列表一次即可(见下面的合并功能)。
归并操作的过程如下:
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
- 重复步骤3直到某一指针到达序列尾
- 将另一序列剩下的所有元素直接复制到合并序列尾
public IList MergeSort(IList a, int low, int height)
{
int l = low;
int h = height;
if (l >= h)
{
return a;
}
int mid = (l + h) / 2;
MergeSort(a, l, mid);
MergeSort(a, mid + 1, h);
int end_lo = mid;
int start_hi = mid + 1;
while ((l <= end_lo) && (start_hi <= h))
{
if (((IComparable)a[l]).CompareTo(a[start_hi]) < 0)
{
l++;
}
else
{
object temp = a[start_hi];
for (int k = start_hi - 1; k >= l; k--)
{
a[k + 1] = a[k];
RedrawItem(k + 1);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
}
a[l] = temp;
RedrawItem(l);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
l++;
end_lo++;
start_hi++;
}
}
return a;
}
| Worst case performance: | O(n log n) |
| Best case performance: | O(n log n) |
| Average case performance: | O(n log n) |
| Worst case space complexity: |
奇偶排序

Odd-even sort is a relatively simple sorting algorithm. It is a comparison sort based on bubble sort with which it shares many characteristics. It functions by comparing all (odd, even)-indexed pairs of adjacent elements in the list and, if a pair is in the wrong order (the first is larger than the second) the elements are switched. The next step repeats this for (even, odd)-indexed pairs (of adjacent elements). Then it alternates between (odd, even) and (even, odd) steps until the list is sorted. It can be thought of as using parallel processors, each using bubble sort but starting at different points in the list (all odd indices for the first step). This sorting algorithm is only marginally more difficult than bubble sort to implement.
奇偶排序是一个相对简单的排序算法。它是一种基于冒泡排序的比较算法,它们有着许多共同点。它通过比较所有相邻的(奇数偶)对进行排序,如果某对存在错误的顺序(第一个元素大于第二个),则交换。下一步针对{偶奇对}重复这一操作。然后序列就在(奇,偶)和(偶,奇)之间变换,直到列表有序。它可以看作是是使用并行处理器,每个都用了冒泡排序,但只是起始点在列表的不同位置(所有奇数位置可做第一步)。这个排序算法实现起来只是略微比冒泡排序复杂一些。
public IList OddEvenSort(IList arrayToSort)
{
bool sorted = false;
while (!sorted)
{
sorted = true;
for (var i = 1; i < arrayToSort.Count - 1; i += 2)
{
if (((IComparable)arrayToSort[i]).CompareTo(arrayToSort[i + 1]) > 0)
{
object temp = arrayToSort[i];
arrayToSort[i] = arrayToSort[i + 1];
RedrawItem(i);
arrayToSort[i + 1] = temp;
RedrawItem(i+1);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
sorted = false;
}
}
for (var i = 0; i < arrayToSort.Count - 1; i += 2)
{
if (((IComparable)arrayToSort[i]).CompareTo(arrayToSort[i + 1]) > 0)
{
object temp = arrayToSort[i];
arrayToSort[i] = arrayToSort[i + 1];
arrayToSort[i + 1] = temp;
RedrawItem(i);
RedrawItem(i+1);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
sorted = false;
}
}
}
return arrayToSort;
}
鸽巢排序
鸽巢排序,也被称为 count sort (不要和 counting sort 搞混了),当数组元素的元素数量(n)和可能的键值数(key value,N)大约相同时,这种排序算法实用。它的时间复杂度为O(n+N)。
(在不可避免遍历每一个元素并且排序的情况下效率最好的一种排序算法。但它只有在差值(或者可被映射在差值)很小的范围内的数值排序的情况下实用。)
算法流程如下:
- Given an array of values to be sorted, set up an auxiliary array of initially empty “pigeonholes”, one pigeonhole for each key through the range of the original array. 假设有个一个待排序的数组,给它建立了一个空的辅助数组(称为“鸽巢”)。把原始数组中的每个值作为一个key(“格子”)。
- Going over the original array, put each value into the pigeonhole corresponding to its key, such that each pigeonhole eventually contains a list of all values with that key. 遍历原始数组,根据每个值放入辅助数组对应的“格子”
- Iterate over the pigeonhole array in order, and put elements from non-empty pigeonholes back into the original array. 顺序遍历“鸽巢”数组(辅助数组),把非空鸽巢中的元素放回原始数组。
public IList PigeonHoleSort(IList list)
{
object min = list[0], max = list[0];
foreach (object x in list)
{
if (((IComparable)min).CompareTo(x) > 0)
{
min = x;
}
if (((IComparable)max).CompareTo(x) < 0)
{
max = x;
}
Thread.Sleep(speed);
}
int size = (int)max - (int)min + 1;
int[] holes = new int[size];
foreach (int x in list)
holes[x - (int)min]++;
int i = 0;
for (int count = 0; count < size; count++)
while (holes[count]-- > 0)
{
list[i] = count + (int)min;
RedrawItem(i);
i++;
RefreshPanel(pnlSamples);
Thread.Sleep(speed);
}
return list;
}
| Worst case performance: | O(n+2k) |
| Best case performance: | - |
| Average case performance: | O(n+2k) |
| Worst case space complexity: | O(2k) |
快速排序

快速排序采用分而治之的策略,把一个列表划分为两个子列表。步骤是:
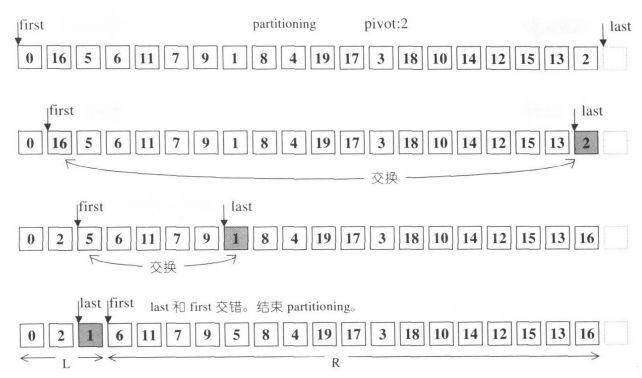
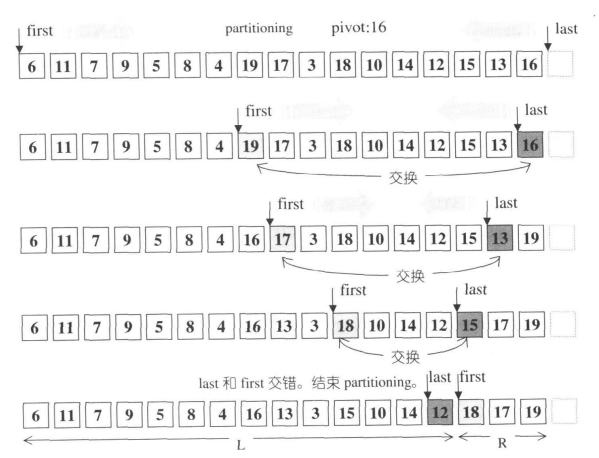
- 从列表中,选择一个元素,称为基准(pivot)。
- 重新排序列表,把所有数值小于枢轴的元素排到基准之前,所有数值大于基准的排基准之后(相等的值可以有较多的选择)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
- 分别递归排序较大元素的子列表和较小的元素的子列表。
递归的结束条件是列表元素为零或一个,即已不需要排序。
public IList QuickSort(IList a, int left, int right)
{
int i = left;
int j = right;
double pivotValue = ((left + right) / 2);
int x = (int)a[int.Parse(pivotValue.ToString())];
while (i <= j)
{
while (((IComparable)a[i]).CompareTo(x) < 0)
{
i++;
}
while (((IComparable)x).CompareTo(a[j]) < 0)
{
j--;
}
if (i <= j)
{
object temp = a[i];
a[i] = a[j];
RedrawItem(i);
i++;
a[j] = temp;
RedrawItem(j);
j--;
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
}
}
if (left < j)
{
QuickSort(a, left, j);
}
if (i < right)
{
QuickSort(a, i, right);
}
return a;
}
| Worst case performance: | O(n2) |
| Best case performance: | O(n log n) |
| Average case performance: | O(n log n) |
| Worst case space complexity: | O(log n) |
使用冒泡的快速排序

public IList BubbleSort(IList arrayToSort, int left, int right)
{
for (int i = left; i < right; i++)
{
for (int j = right; j > i; j--)
{
if (((IComparable)arrayToSort[j - 1]).CompareTo(arrayToSort[j]) > 0)
{
object temp = arrayToSort[j - 1];
arrayToSort[j - 1] = arrayToSort[j];
RedrawItem(j-1);
arrayToSort[j] = temp;
RedrawItem(j);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
}
}
}
return arrayToSort;
}
public IList QuickSortWithBubbleSort(IList a, int left, int right)
{
int i = left;
int j = right;
if (right - left <= 6)
{
BubbleSort(a, left, right);
return a;
}
double pivotValue = ((left + right) / 2);
int x = (int)a[int.Parse(pivotValue.ToString())];
a[(left + right) / 2] = a[right];
a[right] = x;
RedrawItem(right);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
while (i <= j)
{
while (((IComparable)a[i]).CompareTo(x) < 0)
{
i++;
}
while (((IComparable)x).CompareTo(a[j]) < 0)
{
j--;
}
if (i <= j)
{
object temp = a[i];
a[i++] = a[j];
RedrawItem(i - 1);
a[j--] = temp;
RedrawItem(j + 1);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
}
}
if (left < j)
{
QuickSortWithBubbleSort(a, left, j);
}
if (i < right)
{
QuickSortWithBubbleSort(a, i, right);
}
return a;
}
选择排序

原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
算法过程如下:
- 找到列表中的最小值,
- 把它和第一个位置的元素交换,
- 列表其余部分重复上面的步骤(从第二个位置开始,且每次加1).
列表被有效地分为两个部分:从左到右的有序部分,和余下待排序部分。
public IList SelectionSort(IList arrayToSort)
{
int min;
for (int i = 0; i < arrayToSort.Count; i++)
{
min = i;
for (int j = i + 1; j < arrayToSort.Count; j++)
{
if (((IComparable)arrayToSort[j]).CompareTo(arrayToSort[min]) < 0)
{
min = j;
}
}
object temp = arrayToSort[i];
arrayToSort[i] = arrayToSort[min];
arrayToSort[min] = temp;
RedrawItem(i);
RedrawItem(min);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
}
return arrayToSort;
}
| Worst case performance: | O(n2) |
| Best case performance: | O(n2) |
| Average case performance: | O(n2) |
| Worst case space complexity: | O(1) |
希尔排序

希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序,算法的最后一步就是普通的插入排序,但是到了这步,需排序的数据几乎是已排好的了(此时插入排序较快)。
假设有一个很小的数据在一个已按升序排好序的数组的末端。如果用复杂度为O(n2)的排序(冒泡排序或插入排序),可能会进行n次的比较和交换才能将该数据移至正确位置。而希尔排序会用较大的步长移动数据,所以小数据只需进行少数比较和交换即可到正确位置。
一个更好理解的希尔排序实现:将数组列在一个表中并对列排序(用插入排序)。重复这过程,不过每次用更长的列来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法,算法本身仅仅对原数组进行排序(通过增加索引的步长,例如是用i += step_size而不是i++)。
例如,假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ],如果我们以步长为5开始进行排序,我们可以通过将这列表放在有5列的表中来更好地描述算法,这样他们就应该看起来是这样:
13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10
然后我们对每列进行排序:
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
将上述四行数字,依序接在一起时我们得到:[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ].这时10已经移至正确位置了,然后再以3为步长进行排序:
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
排序之后变为:
10 14 13 25 23 33 27 25 59 39 65 73 45 94 82 94
最后以1步长进行排序(此时就是简单的插入排序了)。
public IList ShellSort(IList arrayToSort)
{
int i, j, increment;
object temp;
increment = arrayToSort.Count / 2;
while (increment > 0)
{
for (i = 0; i < arrayToSort.Count; i++)
{
j = i;
temp = arrayToSort[i];
while ((j >= increment) &&
(((IComparable)arrayToSort[j - increment]).CompareTo(temp) > 0))
{
arrayToSort[j] = arrayToSort[j - increment];
RedrawItem(j);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
j = j - increment;
}
arrayToSort[j] = temp;
RedrawItem(j);
pnlSamples.Refresh();
if (chkCreateAnimation.Checked)
SavePicture();
}
if (increment == 2)
increment = 1;
else
increment = increment * 5 / 11;
}
return arrayToSort;
}
| Worst case performance: | - |
| Best case performance: | n |
| Average case performance: | O(n log2 n) |
| Worst case space complexity: | O(1) |
最后,感谢给与我帮助的人,有了你们的帮助,本文的质量有了更大的提高,谢谢!

 0
0
 0
0













 这几天系统地学习了一下
这几天系统地学习了一下